Dynamic Programming-3
동적계획법
1. 일반적으로 최적화문제(optimisation problem) 혹은 카운팅(counting) 문제에 적용된다.
2. 주어진 문제에 대한 순환식(recurrence equation)을 정의한다.
3. 순환식을 memoization 혹은 bottom-up 방식으로 푼다.
최적화문제는 최솟값이나 최댓값 구하는 경우 또는 최단 경로 문제.
카운팅 문제는 어떤 특정한 해의 개수를 구하는 문제.
- subproblem들을 풀어서 원래 문제를 푸는 방식. 그런 의미에서 분할정복법과 공통성이 있음.
- 분할정복법에서는 분활된 문제들이 서로 disjoint하지만 동적계획법에서는 그렇지 않음.
- 즉 서로 overlapping하는 subproblem들을 해결함으로써 원래 문제를 해결.
그렇다면 분할정복법과 동적계획법의 차이에 대해 더 자세히 알아보도록 하자.
분할정복법

quicksort의 경우, pivot을 기준으로 분활된 두 subproblem은 서로 disjoint하다.
동적계획법

Optimal Substructure
- 어떤 문제의 최적해가 그것의 subproblem들의 최적해로부터 효율적으로 구해질 수 있을 때 그 문제는 optimal substructure를 가진다고 말한다.
- 분할정복법, 탐욕적기법, 동적계획법은 모두 문제가 가진 이런 특성을 이용한다.

Optimal Substructure를 확인하기 위해서는 "최적해의 일부분이 그 부분에 대한 최적해인가?"라는 질문을 만족해야 한다.
그렇다면, 최장경로 문제도 앞의 순환식과 같은 방식으로 표현할 수 있을까?
최장경로 문제
노드를 중복 방문하지 않고 가는 가장 긴 경로
optimal substructure를 가지는가?
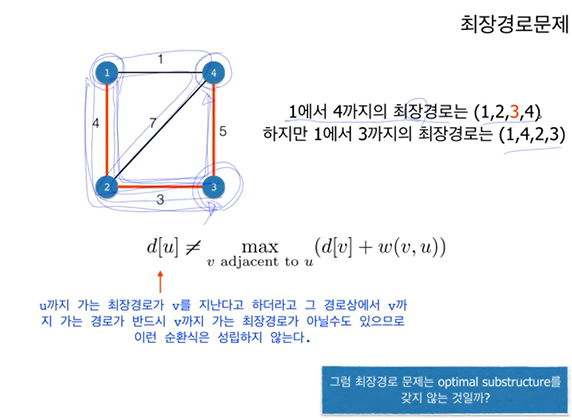

마지막 경우는 s에서 u까지 A에 속한 노드들과 동시 v모두 지나지 않고 가는 최장 경로 길이+ w(u,v)를 나타낸다.
즉, 최장경로 문제는 다른 형태의 optimal substucture를 가지는 것일 뿐 optimal substructure를 가지지 않는다고 말할 수는 없다.
Dynamic Programming-4 : Matrix-Chain Multiplication
pxq 행렬 A와 qxr 행렬 B를 곱할 때의 코드이다.
void product(int A[][], int B[][], int C[][]){
for(int i=0;i<p;i++){
for(int j=0;j<r;j++){
C[i][j] = 0;
for(int k=0; k<q;k++)
C[i][j] += A[i][k]*B[k][j];
}
}
}
pxq행렬과 qxr 행렬을 곱하면 q가 중복되므로 pxr행렬이 만들어진다.

곱셈연산의 횟수=pqr
Matrix-Chain 곱하기
행렬 A는 10x100, B는 100x5, C는 5x50
세 행렬의 곱 ABC는 두 가지 방법으로 계산가능(결합법칙이 성립)
(AB)C: 7,500번의 곱셉이 필요(10x100x5 + 10x5x50)
A(BC): 75,000번의 곱셉이 필요(100x5x50 + 10x100x50)
즉 곱하는 순서에 따라서 연산량이 다름
n개의 행렬의 곱 A1A2A3...An을 계산하는 최적의 순서는?
여기서 Ai는 p(k-1)xp(k)행렬이다.


Ai...Ak를 곱하면 pk-1pk가 만들어지고, Ak+1...Aj를 곱하면 pkpj가 만들어지므로 pi-1pkpj가 뒷부분에 붙는다.
계산 순서


int matrixChain(int n)
{
for(int i=1;i<=n;i++)
m[i][i] = 0; //대각선을 0으로 채우기
for(int r=1;r<=n-1;r++){ //채워야 할 대각선의 개수가 n-1개여서
for(int i=1; i<=n-r;i++){ //각 대각선의 값의 개수
//r번째 대각선의 i번째 값
int j=i+r;
m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j];
for(int k=i+1;k<=j-1;k++){
if(m[i][j] > m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j])
m[i][j] = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
}
}
}
return m[1][n];
}시간복잡도 n의 3승
Dynamic Programming-5 : Longest Common Subsequence(LCS)
<bcdb>는 문자열 <abcbdab>의 subsequence이다.
<bca>는 문자열 <abcbdab>와 <bdcaba>의 common subsequence이다.
Longest Common Subsequence(LCS)는
입력으로 2개의 문자열이 들어올 때, 두 문자열의 common subsequence중 가장 긴 것을 찾는 문제이다.
<bcba>는 <abcbdab>와 <bdcaba>의 LCS이다.

순환식




int lcs(int m, int n) //m:length of X, n: length of Y
{
for(int i=0;i<=m;i++)
c[i][0] = 0;
for(int j=0;j<=n;j++)
c[0][j] = 0;
for(int i=0;i<=m;i++){
for(int j=0;j<=n;j++){
if(x[i] == y[j])
c[i][j] = c[i-1][j-1] + 1;
else
c[i][j] = Math.max(c[i-1][j], c[i][j-1]);
}
}
return c[m][n];
}시간 복잡도는 mn
'스터디 > 2024하계모각코' 카테고리의 다른 글
| [2024하계모각코] 4주차 결과 (2) | 2024.07.24 |
|---|---|
| [2024 하계모각코] 4주차 목표 (0) | 2024.07.24 |
| [2024 하계모각코] 3주차 목표 (0) | 2024.07.15 |
| [2024 하계모각코] 2주차 결과 (1) | 2024.07.08 |
| [2024 하계모각코] 2주차 목표 (0) | 2024.07.08 |